
Data Integrity: CRC with Kotlin on Android
When working with any communication or storage medium such as Bluetooth, wi-fi (and even wired networks) or disk storage, data can get corrupted. In such cases, we need to make sure that the data we receive (or read) is the same data that was sent (or written). We need a mechanism to validate the integrity of the data.
There are many ways to accomplish this. The most common one is called Cyclic Redundancy Check (CRC). CRC is like a checksum that is appended to the data. It enables us to detect any unwanted changes in the transmitted or stored data.
Understanding the maths behind the CRC is a little challenging. But if you want to take a deep dive, we’ve got another article for you which covers all the theory and explains in detail how a CRC works. In this article, we will solely focus on the implementation of a CRC algorithm in Kotlin, for use in Android app development.
There are different kinds of CRCs that vary in their bit size. Common ones are CRC-8, CRC-16 and CRC-32. CRCs with larger bit sizes detect more errors, but come at the price of taking up more storage space. As an iOS or macOS developer, you will most likely not be the one to make this decision. A specific CRC bit size will most likely be required by the hardware you interact with.
Let’s first start with a simple way to calculate a CRC-32 for a given data array by using existing functionality. We’ll then move on to implement our own algorithm to calculate a CRC-16, which can be easily adapted for any CRC bit size.
Calculating a 32-bit CRC in Kotlin
Java provides a built-in class to calculate the CRC-32 of any sequence of bytes. This CRC32 class can be used in Kotlin as well. It’s part of the package java.util.zip.
Let’s assume we have the following 7 bytes of data for which we want to calculate the CRC-32:
val input = byteArrayOf(-44, 125, 31, -36, 15, 99)
To do that, we first need to create an instance of the CRC32 class:
val crc32 = CRC32()
Computing the CRC is now as simple as this:
crc32.update(input) crc32.value // returns 3873799252
The method is called update because you could use the same CRC32 instance to compute a single CRC for multiple inputs. In this case, we only have one input and value returns the CRC for it. You can read more about the CRC32 in the Android Documentation.
Unfortunately, this is the only CRC function available in this package. There is no function included for calculating any other type of CRC (such as CRC-8 or CRC-16) or any other variant of CRC-32 (with a different polynomial). For that reason, we’ll write our own implementation of a CRC function in the remaining sections of this article.
ℹ️ Note: There is also an implementation of CRC-16 in sun.misc but Oracle discourages using sun packages as their API might change and they might not be available on all JVMs.
Calculating a 16-bit CRC in Kotlin
While there is only one distinct mathematical foundation behind the concept of a CRC, there are different ways to calculate it in Kotlin. We’ll start with the simplest implementation in order to understand how it works, assuming that we only have a single byte for which we calculate the CRC-16. We’ll then move on to generalize our solution for an arbitrary number of bytes, using an efficient algorithm.
The CRC-16 for a Single Byte
Let’s begin by specifying the requirements of our CRC-16 function: First of all, we need some input data on which we want to compute the CRC. We’ll start with a single byte of data (UByte) and will later expand the algorithm to work for any number of bytes. To compute the CRC, we also need to choose a polynomial suited for our use case. (That’s a topic of its own and we won’t go into detail on how to pick a suitable polynomial as it will usually be predefined by the systems you interact with.)
As we want to have a CRC-16, we need an output of the same size (16 bits), so we pick a UShort. The polynomial must have the same size:
- Inputs:
- input: 1 Byte →
UByte - polynomial: 2 Bytes →
UShort
- input: 1 Byte →
- Outputs:
- crc: 2 Bytes →
UShort
- crc: 2 Bytes →
Now, let’s define a function based on these inputs and outputs:
fun crc16(input: UByte, polynomial: UShort): UShort
Since unsigned types are experimental in Kotlin (meaning that they are stable, but their API might change), we recommend to add the @ExperimentalUnsignedTypes annotation wherever you use those types. We will not use these annotations in this article in order to stay focused on the actual implementation.
Now comes our first little obstacle: the endianness – in other words: the order of bytes. Most platforms use the little-endian format to store integers in memory, meaning that the most significant byte is at the end. (You can verify that with the isLittleEndian property of the platform as explained in the Kotlin documentation.) However, we’ll be using the big-endian format in our algorithm. Thus, whenever we work with integers larger than 1 byte, we first need to reverse their byte order. So, we first convert the input to 16-bit (UShort) and then effectively swap the two bytes with a left-shift by 1 byte (= 8 bit).
val bigEndianInput = input.toUShort() shl 8
Unfortunately, there is no bitwise shift operator for unsigned types in Kotlin. So we need to implement the shl infix operator ourselves as an extension function on UShort:
infix fun UShort.shl(bitCount: Int): UShort =
(this.toUInt() shl bitCount).toUShort()
Here’s a visual representation of how we convert our UByte input into a 2-byte UShort value in big-endian representation:
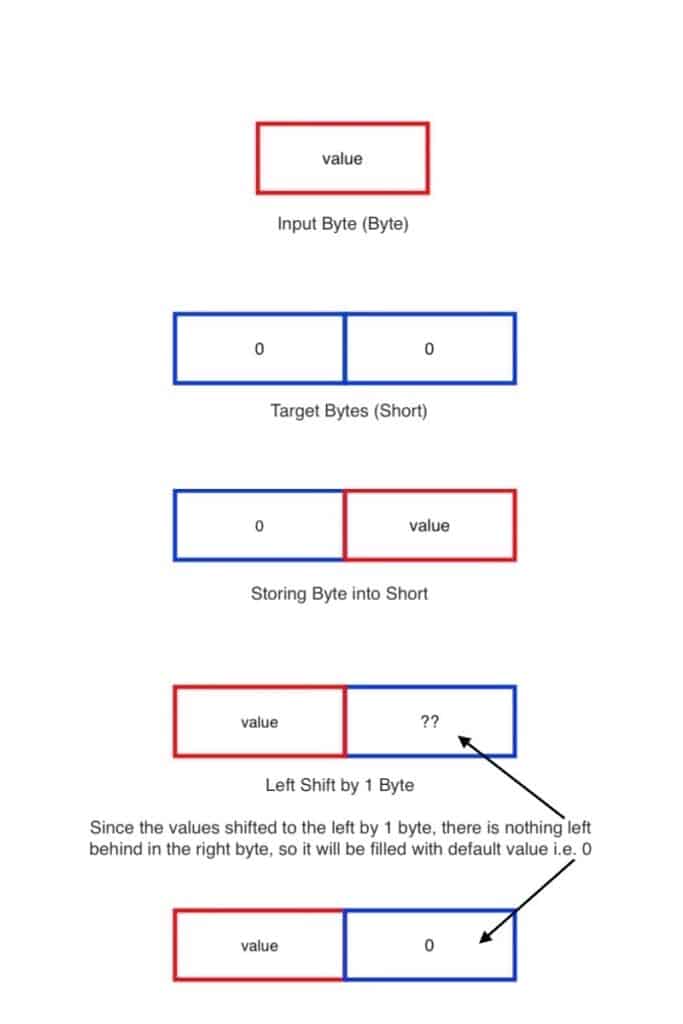
Now that we have the input data in the right format, let’s begin with the actual calculation of the CRC. We will use a variable result to store the intermediate results of our calculation and initially set it to the bigEndianInput from above:
var result = bigEndianInput
Next, we need to perform the following operations on each bit of the input. Since our function calculates the CRC of 1 byte, we need to perform these operations 8 times:
- Check if the most significant bit of the current
resultis 1. To get the most significant bit in big-endian format, we simply perform a logical and operation with a value of the same bit size, that has a 1 in its first (= most significant) bit and 0s in all other bits:- for 8-bit CRCs, we use
10000000, in hexadecimal:0x80 - for 16-bit CRCs, we use
10000000 00000000, in hexadecimal:0x8000 - etc.
- for 8-bit CRCs, we use
val isMostSignificantBitOne = result and 0x8000.toUShort() != 0.toUShort()
- Shift the
resultto the left by 1 bit.
result = result shl 1
- If the most significant bit computed in step (1) was 1, we perform an XOR operation on the
resultand thepolynomial. (From a mathematical perspective, we subtract the polynomial from the result. In binary representation, this is equivalent to the XOR operation.)
if (isMostSignificantBitOne) {
result = result xor polynomial
}
ℹ️ Note: The algorithm to compute a CRC is based on a polynomial division with modulo-2. If you want to know how this works in detail, we’ve explained how this works in our generic article on CRCs. For the scope of this article, suffice it to say that the modulo-2 division is a combination of left-shifts and XOR operations. That’s what we do here.
As mentioned before, we need to perform the above three operations on each bit (i.e. 8 times), so putting the pieces together, we end up with this function:
fun crc16(input: UByte, polynomial: UShort): UShort {
val bigEndianInput = input.toUShort() shl 8
var result = bigEndianInput
for(i in 0 until 8) {
val isMostSignificantBitOne =
result and 0x8000.toUShort() != 0.toUShort()
result = result shl 1
if (isMostSignificantBitOne) {
result = result xor polynomial
}
}
return result
}
We can also write this function a little more elegantly using fold instead of a for loop:
fun crc16(input: UByte, polynomial: UShort): UShort {
val bigEndianInput = input.toUShort() shl 8
return (0 until 8).fold(bigEndianInput) { result, _ ->
val isMostSignificantBitOne =
result and 0x8000.toUShort() != 0.toUShort()
val shiftedResult = result shl 1
when (isMostSignificantBitOne) {
true -> shiftedResult xor polynomial
false -> shiftedResult
}
}
}
The CRC-16 for an Array of Bytes
The above algorithm works well and we could easily adapt it for other CRC sizes, using the same “recipe”. However, this function might become very slow, especially for larger CRCs and large byte arrays of input data. Fortunately, there is a mathematical trick we can apply to make the computation much more efficient.
CRC computation is slow because we have to go through each bit of every byte. For example, if you have an array with 128 bytes, you would need to iterate 8 ⨉ 128 = 1024 times. Now imagine a much longer array, it will need a lot of more iterations.
So how do we make the computation faster? The solution is to precompute a part of the algorithm that will always be the same, regardless of the number of input bytes. This precomputed part is then stored in an array (also called a look-up table).
The CRC is the remainder of a long division of the input bytes (dividend) and the polynomial (divisor). During that division, we have to go through all the bytes of the input. But instead of looping through each bit of each byte of the input, we now use our look-up table which contains the CRC values for every possible value of a single byte (0-255). This saves us a lot of computing power and makes our calculation much faster.
Generating a CRC Look-up Table
- First, we need to choose a polynomial.
A different polynomial will yield a different CRC value for the same input. In this example, we choose a very commonly used CRC-16 polynomial:
x16 + x12 + x5 + 1
(It’s called CRC16-CCITT.) - Next, we convert the polynomial to its binary representation:
10001000000100001
If this seems like magic, we have to disappoint you – it’s really pretty simple and straight-forward: Starting from the highest exponent, go through all exponents in decreasing order. Put a1for all exponents that are present and0for the missing ones. That’s how you end up with the binary representation of the polynomial. - The resulting polynomial has 17 bits. Based on the mathematical properties of the CRC polynomials, we can discard the most significant bit (equivalent to a left-shift by 1 bit in big-endian representation) to make it a 16-bit polynomial:
0001000000100001 - We convert these 16 bits into their hexadecimal representation:
0x1021 - Now we use this polynomial representation to generate the CRC for each possible byte value. The resulting array is our lookup-table:
val crc16Table = (0 until 256).map {
crc16(it.toUByte(), 0x1021.toUShort())
}
Calculating the CRC with a Look-up Table
Using the CRC-16 table from above, we can easily calculate the CRC for any number of bytes. We go through the input bytes one by one and make use of the precomputed values.
fun crc16(inputs: UByteArray): UShort {
return inputs.fold(0.toUShort()) { remainder, byte ->
val bigEndianInput = byte.toUShort() shl 8
val index = (bigEndianInput xor remainder) shr 8
crc16Table[index.toInt()] xor (remainder shl 8)
}
}
To understand the code in detail, you need some mathematical background on how the algorithm is derived (not part of this article). The core learning here is that we iterate over the input data byte-wise rather than bit-wise. That’s why this algorithm is much more efficient for long data streams.
As you might have noticed, we used a bitwise right-shift operator (shr) in the algorithm, which is also not available for unsigned integer types in Kotlin. Thus, we implement it ourselves the same way we implemented the left-shift operator (shl):
infix fun UShort.shr(bitCount: Int): UShort =
(this.toUInt() shr bitCount).toUShort()
For convenience, let’s also create a function that takes a ByteArray as an input parameter:
fun crc16(inputs: ByteArray): UShort =
crc16(inputs.map(Byte::toUByte).toUByteArray())
One drawback of this method is that we always need to compute the CRC for the entire input data all at once. But oftentimes, we might have a number of smaller arrays for which we want to compute only one CRC. Using the above function, we would have to combine all of those smaller data arrays into one big array.
Instead, let’s make our lives a little easier and slightly modify our crc16 function so that we can compute the final CRC in chunks:
fun crc16(inputs: UByteArray, initialValue: UShort = 0.toUShort()): UShort {
return inputs.fold(initialValue) { remainder, byte ->
val bigEndianInput = byte.toUShort() shl 8
val index = (bigEndianInput xor remainder) shr 8
crc16Table[index.toInt()] xor (remainder shl 8)
}
}
We only changed two things:
- We added a new parameter
initialValue(with a default value of 0). - We replaced
inputs.fold(0.toUShort())withinputs.fold(initialValue).
With these changes, we can compute a CRC for multiple byte arrays step-by-step. But let’s not forget to adapt our convenience method accordingly:
fun crc16(inputs: ByteArray, initialValue: Short = 0): UShort =
crc16(inputs.map(Byte::toUByte).toUByteArray(), initialValue.toUShort())
Example
Given the following input array of 5 bytes
byteArrayOf(1, 2, -16, 125, 3)
we can calculate their CRC-16 like this:
crc16(listOf(1, 2, 240, 125, 3).map(Int::toUByte).toUByteArray()) // returns 59917
Using our convenience method, the code looks a bit prettier:
crc16(byteArrayOf(1, 2, -16, 125, 3)) // returns 59917
Alternatively, we can also split the input array and compute the CRC-16 in two steps:
val initialCRC = crc16(byteArrayOf(1, 2)) // returns 4979 crc16(listOf(240, 125, 3).map(Int::toUByte).toUByteArray(), initialCRC) // returns 59917
That’s almost the same concept as used by the CRC-32 class in the java.util.zip package that we introduced in the beginning:
val crc32 = CRC32()
The only difference is that the crc32 instance stores the “initial value” for the next CRC calculation internally:
val firstInput: ByteArray = byteArrayOf(-44, 125, 31) // -44 is 212 (unsigned byte) val secondInput: ByteArray = byteArrayOf(-36, 15, 99) // -36 is 220 (unsigned byte) crc32.update(firstInput) crc32.update(secondInput) crc32.value // returns 3873799252
Conclusion
In this article, you’ve learned how to compute 16- and 32-bit CRCs in Kotlin. We used Java’s existing implementation for easily retrieving the CRC-32 for a variable-length byte array. We then explained how we can write our own implementation to calculate any type of CRC. You should now be able to
- generate a CRC table for any type of CRC (and any type of polynomial)
- (efficiently) calculate any type of CRC for a byte array of an arbitrary size
Where to go from here
- You can find all the CRC implementations (and some additional ones!) in our Kotlin CRC repository.
- If you want to understand how the CRC works in more detail, please check our article on How to validate your Data with a Cyclic Redundancy Check.
- We also have an article with the respective CRC implementations in Swift for iOS and macOS developers.

