How to Validate Your Data with a Cyclic Redundancy Check (CRC)

NOVEMBER 13, 2020 | GHULAM NASIR

The cool thing about programming is that there is an absolute truth in every Bit: It’s either black or white, 1 or 0, true or false. In theory. But whenever you transmit data or store it somewhere on a physical drive, it can get corrupted. Individual bits can get flipped or even bursts of multiple bits, changing the value and the meaning of your data inadvertently. Surrounding electromagnetic radiation can interfere with your Bluetooth or wi-fi signals and cause unintended changes in your data stream. Simply accessing a flash memory might also result in bit flips.

So whenever you exchange data with other systems, how do you make sure that the data you receive is exactly the same as the data that was sent to you? How do you detect accidental changes in your data stream? Or in other words, how do you check the integrity of your data against unintended changes and losses?

There are a number of mechanisms used for data error detection. The most common one is called Cyclic Redundancy Check (CRC). It is often used in Bluetooth and other wireless communication protocols. It is also used to check the integrity of different types of files such as Gzip, Bzip2, PNG etc. The name sounds rather complex and intimidating. However, after reading this article you should have a good understanding of what a CRC is and how it works.

The Basics

CRC is an error detection code used for verifying the integrity of data. It works just like a checksum and is appended to the end of the payload data and transmitted (or stored) along with that data.

For example, let’s say we want to send the lower-case letter z to someone else. In Unicode, the z is represented by the number 0x7A, that’s 0111 1010 in binary representation. In order to make it possible for the receiver to verify that the data wasn’t modified on transmission, we calculate the CRC for this data (1000) and simply append it to our message:

0111 1010 (data) → 0111 1010 1000 (data + CRC)

The check value is called redundant because it doesn’t add any additional information to the message. (This data is only appended for the sake of error detection and data integrity). 0111 1010 contains the same information as 0111 1010 1000 (where last 4 bits are the CRC), however, in the first case, the receiver has no way of verifying if the data was received correctly.

CRCs are specifically designed to detect common data communication errors. It can also detect when the order of the bits or bytes changes. CRCs can easily be implemented in hardware – another reason for their widespread use. Before we take a deep dive into how a CRC works, there is one important concept that we need to understand first: The endianness.

Endianness

The endianness is the order of bytes with which data words are stored. We distinguish the following to types:

Little-endian: The least significant byte is stored at the smallest memory address. In terms of data transmission, the least significant byte is transmitted first.
Big-endian: The most significant byte is stored at the smallest memory address. In terms of data transmission, the most significant byte is transmitted first.

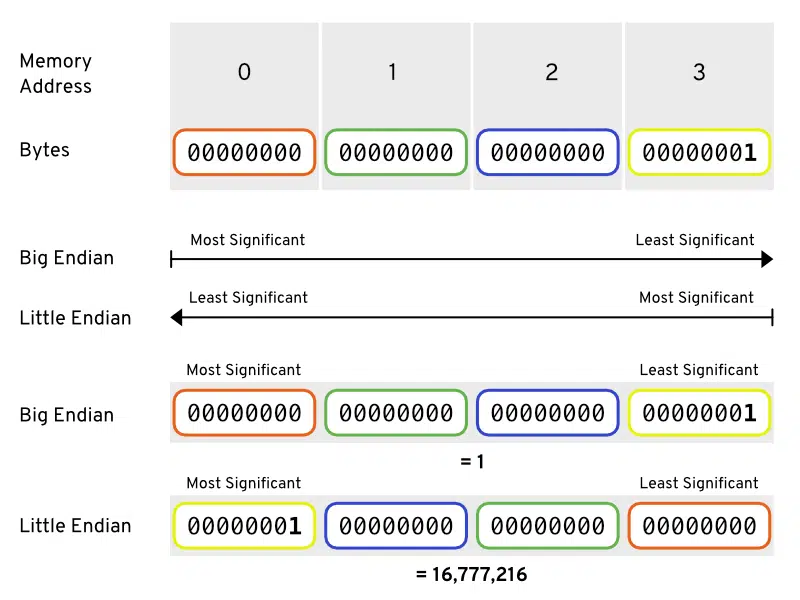
In the introductory example (with the letter z), we only used a CRC with a size of 1 byte, so the endianness doesn’t matter in this case. However, in many cases, we use CRCs that consist of mulitple bytes. So the question arises which endianness to use for CRC?

From an app developer’s perspective, the answer is quite simple: We use the same endianness as the system we want to communicate with. It’s usually required by the hardware to use a particular byte order. For the remainder of this article, we’ll stick with the big-endian format and provide some hints along the way on how a little-endian implementation would differ.

The Concept of a CRC

Mathematically spoken, a CRC is the remainder of a modulo-2 polynomial division of the data. So, the CRC can be written as

CRC = data %

₂

 polynomial

The polynomial can be any mathematical polynomial (without any coefficients) up to the order of the CRC bit size. So if we want a CRC with 8 bits, the highest exponent of the polynomial must be 8 as well. Example:

x⁸ + x² + x + 1

As you can imagine from the simple equation above, choosing a different polynomial will result in a different CRC for the same data. So sender and receiver need to agree on a common polynomial, or else they will always end up with a different CRC and assume that the data got corrupted on the way. Depending on the use case, some polynomials are better suited than others. (Picking the right one is a topic on its own and beyond the scope of this article.)

Any such polynomial can be represented in binary form by going through the exponents from highest to lowest and writing a 1 for each exponent that is present (8, 2, 1 and 0 in our example) and a 0 for each absent exponent (7, 6, 5, 4, 3 in this case):

Exponent    8 7 6 5 4 3 2 1 0
Polynomial  1 0 0 0 0 0 1 1 1 
–––––––––––––––––––––––––––––
Bit Index   0 1 2 3 4 5 6 7 8

The above is the big-endian representation of the polynomial. For its little-endian representation, simply reverse the order of bits:

Exponent    0 1 2 3 4 5 6 7 8
Polynomial  1 1 1 0 0 0 0 0 1 
–––––––––––––––––––––––––––––
Bit Index   0 1 2 3 4 5 6 7 8

Here are some example polynomials with their (big-endian) binary representation:

Polynomial	Binary Representation
x⁴ + x² + x + 1	`10111`
x⁴ + x³ + x² + 1	`11101`
x⁸ + x⁴ + x² + 1	`100010101`

Next, in order to be able to calculate a CRC, we need to understand the modulo-2 division.

Making Calculations in Modulo-2 Arithmetic

Modulo-2 arithmetic is performed digit by digit (bit by bit) on binary numbers. There is no carry or borrowing in this arithmetic. Each digit is considered independent from its neighbours.

Addition & Subtraction

The curious thing about modulo-2 arithmetic is that both addition and subtraction yield the same result.

  10          10
+ 11        - 11
-----       ------
  01          01

The sum or the difference of two bits can be computed with an XOR operation: The result is 1 if exactly one of the two bits is 1, otherwise the result is 0. As there is no carry or borrowing, the same applies not only for individual bits, but for binary numbers of any length, for example:

  10  +  11
= 10  -  11
= 10 XOR 11
= 01

We get this result by applying the XOR operator on each pair of bits individually:

1 XOR 1 =  0
0 XOR 1 =  1
         -----
          01

Division

Modulo-2 division is performed similarly to “normal” arithmetic division. The only difference is that we use modulo-2 subtraction (XOR) instead of arithmetic subtraction for calculating the remainders in each step.

⚠️ If you are German, please note that in English literature, the divisor 11011 is written first, followed by the dividend 01111010. (In German literature it’s usually the other way around.) The result of the division (quotient) is written on top of the calculation, the remainder at the bottom.

       01011 ⬅︎ Quotient
      ––––––––––––––––––
11011 | 01111010
      - 00000
      ----------
         1111010
       - 11011
       ---------
          010110
        - 00000
        --------
           10110
         - 11011
         -------
            11010
          - 11011
          -------
            0001 ⬅︎ Remainder (mod-2)

Types of CRCs

There are different types of CRCs. They are categorized by the degree of the polynomial they use. As the first exponent of a polynomial of degree n is always present by definition (otherwise it would have a lower degree), its binary representation always begins with a 1. In other words, the first bit of a binary polynomial representation doesn’t carry any information about the polynomial when we agree on a fixed degree.

For that reason, the first bit of a binary polynomial representation is always dropped when computing a CRC in software. So the bit size of the resulting binary representation is always n for a polynomial of degree n. Example:

Polynomial	Binary Representation	Binary (1^st bit dropped)	Bit Size
x⁴ + x² + x + 1	`10111`	`0111`	4
x⁴ + x³ + x² + 1	`11101`	`1101`	4
x⁸ + x⁴ + x² + 1	`100010101`	`00010101`	8

CRCs types are named by their bit size. Here are the most common ones:

CRC-8
CRC-16
CRC-32
CRC-64
CRC-1 (parity bit) is a special case

Generally, we can refer to a CRC as CRC-n, where n is the number of CRC bits and the number of bits of the polynomial’s binary representation with a dropped first bit. Obviously, different CRCs are possible for the same n as multiple polynomials exist for the same degree.

For example, if we want to calculate the CRC-8 for these bits:

01000001

the result looks different, depending on the polynomial we use:

Binary Polynomial (1^st bit dropped)	CRC-8
`110100111`	`11001100`
`100000111`	`11000000`
`101001001`	`01100110`
`111010101`	`01001000`

Above are the standard CRC-8 polynomials used in different applications such as Bluetooth, GSM-B, etc.

Developer as a Service: Extend the Developer Team of your Company

Do you need mobile engineers who care about good software engineering practices? Extend your existing team with our mobile engineers.
Contact us here for an initial consultation session.

🇩🇪 Quality Made in Germany 🇩🇪

Error Detection

How do we choose a suitable CRC and a respective polynomial? There are three things we need to consider:

Random Error Detection Accuracy
Burst Error Detection Accuracy
The Redundancy Factor

Random Error Detection Accuracy

Random errors are errors that can occur randomly in any data. For example, a single bit is flipped when transmitting data or a few bits are lost during the transmission.

Depending on the bit size of the CRC we use, we can detect most of these random errors. However, for a CRC-n, 1/2ⁿ of these errors cannot be detected. The following table shows the percentage of the possible random errors that remain undetected for each CRC type:

CRC Type	Undetected Errors	% Undetected
CRC-8	1/2⁸	0.39
CRC-16	1/2¹⁶	0.0015
CRC-32	1/2³²	0.00000002
CRC-64	1/2⁶⁴	5.4 x 10^-20

Burst Error Detection Accuracy

Errors in data transmission are oftentimes not random but produced over a consecutive sequence of bits. Such errors are called burst errors. They are the most common errors in data communication.

It’s one of the CRC’s strongest properties to detecting burst errors reliably. A CRC-n can detect single burst errors with a maximum length of n bits. However, this depends a lot on the polynomial used for computing the CRC. Some polynomials are able to detect multiple bursts of errors in the transmitted data.

CRC Type	Burst Error Detection
CRC-8	at least a single burst of <= 8 bits
CRC-16	at least a single burst of <= 16 bits
CRC-32	at least a single burst of <= 32 bits
CRC-64	at least a single burst of <= 64 bits

The Redundancy Factor

Using a CRC for error detection comes at the cost of extra (non-meaningful) data. When we use a CRC-32 (4 bytes), we need to transmit two more bytes of “unnecessary” data as compared to a CRC-16. CRCs with a lower bit size are obviously cheaper with respect to storage space.

Based on these three factors, we can decide which CRC type to choose for our application. However, the polynomial you choose for your CRC also affects the efficiency and quality of your error detection. But that’s a topic for itself and we won’t cover it in this article. Fortunately, there are a couple of standard polynomials used for a particular CRC type and in most cases it makes sense to just use one of these.

How It Works: The CRC Algorithm

This section will take you through the steps of calculating a CRC-n for any input data. We will first explain the algorithm and then follow these steps to calculate a 4-bit CRC of some sample data.

Take the CRC polynomial and remove the most significant bit.
Example: 10011 ➔ 0011
Append n zeros to the input.
We call this input the remainder (as it will be the remainder of our binary division after every step and finally becomes the CRC when division is no longer possible).
Remember the most significant bit.
Example: 1010 ➔ most significant bit = 1
Discard the most significant bit.
Example: 1010 ➔ 010
Depending on the most significant bit from step 3, do the following:
- 0 ➔ do nothing (same as subtracting 0 from the remainder)
- 1 ➔ subtract the divisor (polynomial) from the remainder
Repeat steps 3 to 5 for all the bits of the message.
The final remainder is the CRC.

Example

Let’s see how this algorithm works in practice and calculate the 4-bit CRC for the binary Unicode representation of the letter z (as introduced at the beginning of this article):

Input Data: 0111 1010

First, we need to choose a suitable polynomial depending on our use case which must used by both the sender and the receiver. For this example, let’s use this one:

Polynomial	Binary Representation	Binary (1^st bit dropped)	Bit Size
x⁴ + x³ + x + 1	`11011`	`1011`	4

We have already performed step (1) of the algorithm in the table above: 1011 is our binary polynomial representation with a dropped most significant bit. Next, let’s go through the remaining steps as part of our modulo-2 division:

       (Quotient is ignored)
       –––––––––––––––––––––
1011 | 01111010              // 1. Polynomial with dropped MSB | Input        
       01111010 0000         // 2. Append 4 zero bits for the CRC

       01111010 0000         // 3. MSB (first bit) = 0
       -------------
        1111010 0000         // 4. Discard the MSB
      - 0000                 // 5. Do nothing (= subtract 0000)
       ––––––––––––––––––
        1111010 0000         // 3. MSB = 1
        ------------
         111010 0000         // 4. Discard the MSB    
       - 1011                // 5. Subtract the polynomial
       ––––––––––––––––––
         010110 0000         // 3. MSB = 0
         -----------
          10110 0000         // 4. Discard the MSB
        - 0000               // 5. Do nothing (= subtract 0000)
       ––––––––––––––––––
          10110 0000         // 3. MSB = 1
          ----------
           0110 0000         // 4. Discard the MSB
         - 1011              // 5. Subtract the polynomial
       ––––––––––––––––––
           1101 0000         // 3. MSB = 1
           ----------
            1010000          // 4. Discard the MSB
          - 1011             // 5. Subtract the polynomial
       ––––––––––––––––––
             0001000         // 3. MSB = 0
             -------
              001000         // 4. Discard the MSB
            - 0000           // 5. Do nothing (= subtract 0000)
       ––––––––––––––––––
              001000         // 3. Check the most significant bit (MSB = 0)
              ------
               01000         // 4. Discard the MSB
             - 0000          // 5. Do nothing (= subtract 0000)
       ––––––––––––––––––
               01000         // 3. MSB = 0
               -----
                1000         // 4. Discard the MSB
              - 0000         // 5.Do nothing (= subtract 0000)
       ––––––––––––––––––
                1000         // 7. Final remainder = CRC

Implementing The Algorithm in Software

Once you’ve understood the algorithm above, it’s pretty straight-forward to implement it in software. The only thing you need to be clear about is whether you implement the CRC with a big-endian or a little-endian representation. In the following, we’ll provide some concrete implementation advice, assuming a big-endian format.

Take the CRC polynomial and remove the most significant bit.
Usually, you do this manually as you only need to do it once.
(For little-endian: Reverse the bits of the resulting value.)
Append n zeros to the input.
Not needed in software.
Remember the most significant bit.
This is equivalent to performing an AND operation with a value that has a 1 as its most significant bit and a 0 in every other bit. (For little-endian: Just do AND 1, regardless of the CRC size.)
Store this value in a variable. Example:
- 8 bits ➔ 1000 0000 ➔ 0x80
- 16 bits ➔ 1000 0000 0000 0000 ➔ 0x800
- 32 bits ➔ 1000 0000 0000 00000000 0000 0000 0000 ➔ 0x8000000
Discard the most significant bit.
This is equivalent to performing a bitwise left-shift.
(For little-endian: Do a bitwise right-shift.)
Depending on the value of the variable stored in step (3), do the following:
- 0 ➔ do nothing
- 1 ➔ perform and XOR operation with the remainder and the polynomial
Repeat Steps 3 to 5 for all the bits of the message.
A simple for loop or any functional construct (e.g. reduce in Swift, fold in Kotlin) will do the job.
The final remainder is the CRC.
That’s the same in software, of course.

The concrete implementation of a CRC algorithm in software always depends on the platform and the programming language you use. If you know how to work with bits and bytes on your respective platform, you should now be able to implement a CRC algorithm of your desired type on your own.

However, if you are an iOS or macOS developer and don’t want to out in all the effort to write your own implementation from scratch, we’ve dedicated another article for implementing a CRC with Swift on iOS. Another article for Android developers on how to implement a CRC in Kotlin is in our pipeline and coming soon. Stay tuned!

Summary

Congratulations! You’ve made it to the end of this article and should now have a broad understanding of what a Cyclic Redundancy Check (CRC) is and how it works. Here’s a short summary of this article:

CRCs are codes that help us in detecting unintended errors in any transmitted or stored data.
Burst errors are very common in data communication.
A CRC-n can detect burst errors up to a size of n bits.
Since the order of the bytes matters when calculating CRC, it can also detect when the sequence of bytes has changed.
Using a different polynomial for a CRC algorithm will result in a different CRC for the same data.
Endianness matters! Using the same polynomial with the opposite endianness will result in a completely different CRC.

Let us finish with some final thoughts on things you should be aware of:

CRC implementations can be made more efficient by pre-calculating a so-called CRC lookup tables. Please check our other CRC articles to see example implementations that make use of such a lookup table.
A CRC is only meant to detect unintended errors or changes to data. It does not provide any protection against malicious changes. If you want to make your data communication secure, you need to use cryptography instead. (A possible attacker can always recalculate the CRC after changing the data.) We’ve published a couple of articles on that topic as well (see below). 😉

Where to Go From Here

If your company needs a team to help you implement CRCs or to develop an app with Bluetooth capabilities, reach out to us at: [email protected]
If you are curious and would like to see a concrete implementation of a CRC algorithm, we’ve got you covered with two other articles:
- Data Integrity: CRC with Swift on iOS
- Data Integrity: CRC with Kotlin on Android
You can also check out our GitHub repository with some sample implementations of CRC functions in Swift.
If you’re not only interested in detecting accidental data transmission errors, but want to make sure that no one else can read or tamper with your sensitive data, read our articles on app security: